Word Embedding (III): GloVe (Global Vectors)
Published:
In this article, we will introduce another prediction-based word vectors, GloVe.
Background
GloVe (Global Vectors) was proposed by Pennington, Socher, and Manning in 2014. It is a new global log-bilinear regression model that combines the advantages of the count-based and prediction-based model we introduced before.
If you are new to word embedding models, feel free to check out my previous post on Count-based Word Vectors and Prediction-based Model: Word2Vec.
Before getting into GloVe, let’s do a quick comparison between count-based model and prediction-based model, so that you can have a better understanding how GloVe innovates.
| Count-based model | Prediction-based model | |
|---|---|---|
| Advantages | easier to understand, faster training, leverage statistical information | capture complex patterns beyond word similarity, improved performance on other tasks |
| Disadvantages | primarily used to capture word similarity, disproportionate importance given to large counts, relatively poor performance on word analogy task | take some time to go through the math, training time scales with corpus size, insufficient use of statistical information (use local context instead of global co-occurrence matrix) |
Realizing the pros and cons of current models, GloVe utilizes the co-occurrence statistics and the log-bilinear model at the same time to achieve more superior performance. In their own words
Our model efficiently leverages statistical information by training only on the nonzero elements in a word-word cooccurrence matrix, rather than on the entire sparse matrix or on individual context windows in a large corpus. The model produces a vector space with meaningful substructure, as evidenced by its performance of 75% on a recent word analogy task. It also outperforms related models on similarity tasks and named entity recognition.
To show the usefulness of co-occurrence matrix, let’s check out an example. 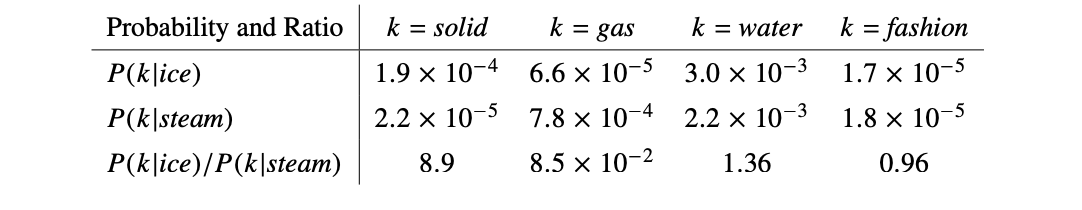
Here “ice” and “steam” are the target words, and we can study their properties using selected context words “solid”, “gas”, “water”, “fashion”. Their co-occurrence probabilities $P(k|ice)$ and $P(k|steam)$ alone are less informative. If you just look at these two rows, you may end up concluding “ice” and “steam” are both most related to “water” and least related to “fashion”. It’s nothing wrong, but it still cannot tell us their differences. But if you check out their co-occurrence ratio $P(k|ice)/P(k|steam)$, a higher value indicates the context word k is more related to “ice” than “steam”. The results are consistent with our common knowledge that ice is solid while steam is gas. For non-discriminative words like “water” and “fashion”, we are likely to get ratios around 1.
You could see the ratios of co-occurrence probabilities entails word meanings. How do we incorporate this information into word vector learning? Let’s get into the model details.
GloVe Model and Performance
The main innovation of GloVe is to link word vectors $w_i$, $w_j$, $\tilde{w_k}$ to the ratios of co-occurrence probabilities $P_{ik}/P_{jk}$. Note here $P_{ik}$ is the same as $P_{i|k}$, and $P_{ik}=X_{ik}/X_{i}$, where $X_{ik}$ is the number of times that word i and k occur together, and $X_{i}$ is the number of times that word i occurs. With this goal in mind, we start with the most general form.
\[F(w_i,w_j,\tilde{w}_k)=\frac{P_{ik}}{P_{jk}}\]Since vector spaces are linear structures, the most natural way is to take vector differences. And we use dot product to avoid mixing vector dimensions in undesirable ways.
\[F((w_i-w_j)^{T}\tilde{w}_k)=\frac{P_{ik}}{P_{jk}}\]In co-occurrence matrix, whether a word is the center word or context word can change arbitrarily. So our final model should be invariant under the exchange of center word $w$ and context word $\tilde{w}$, as well as count matrix $X$ and $X^T$. We achieve this with the form below.
\[F((w_i-w_j)^{T}\tilde{w}_k)=\frac{F(w_i^T \tilde{w}_k)}{F(w_j^T \tilde{w}_k)}=\frac{P_{ik}}{P_{jk}}\] \[F(w_i^T \tilde{w}_k)=exp(w_i^T \tilde{w}_k)=P_{ik}=\frac{X_{ik}}{X_{i}}\] \[w_i^T \tilde{w}_k=log(P_{ik})=log(X_{ik})-log(X_i)\]To restore the symmetry in (5), we add bias term ($b_i$ and $\tilde{b_k}$) for $w_i$ and $\tilde{w_k}$ respectively.
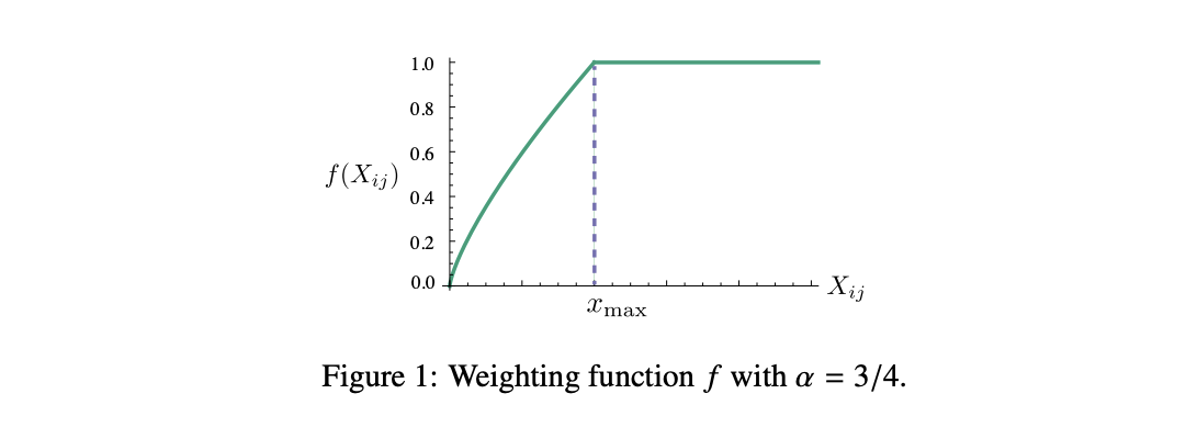
\[w_i^T \tilde{w}_k+b_i+\tilde{b}_k=log(X_{ik})\]The final step towards the loss function is to add a weighting function $f(X_{ij})$, which increases monotonically with the maximum capped at 1. Namely, it assigns higher weight to the more frequent co-occurrences, but capped at 1 to avoid overweighting.
\[f(x)=\begin{cases} (x/x_{max})^{\alpha}\ & if\ x<x_{max} \\ 1 & otherwise \end{cases}\]where the paper use $x_{max}=100$, $\alpha=3/4$.
That’s the main part of the model and you can find a more detailed description in the section 3 of the original paper.
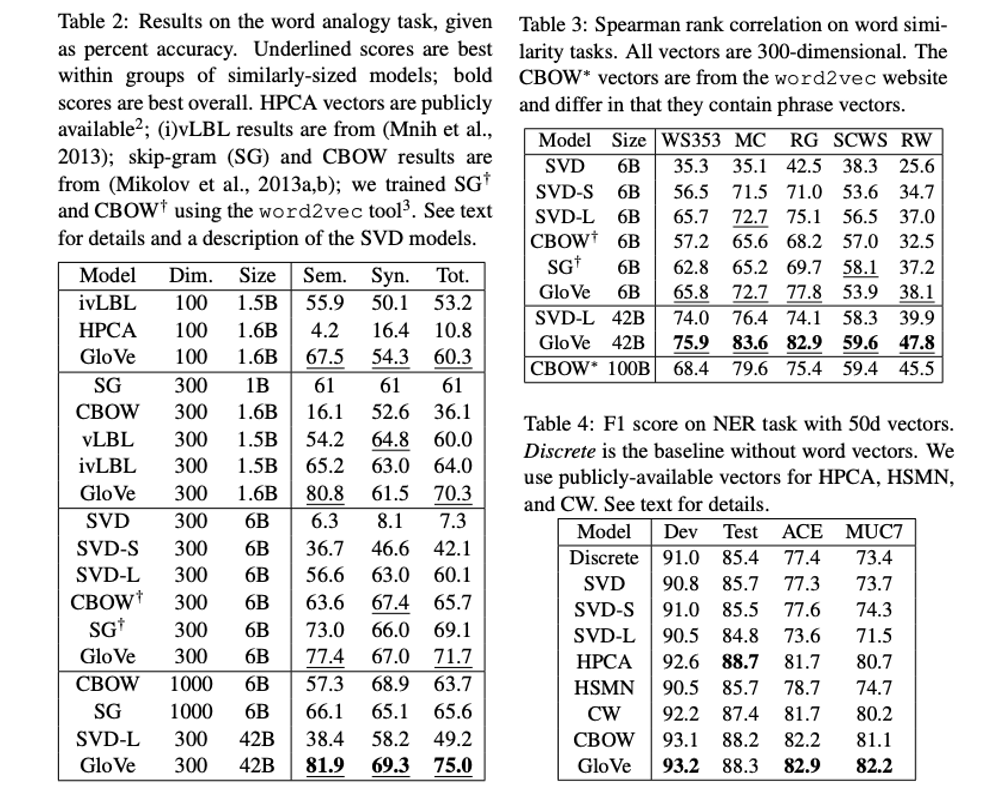
In the remaining part, they consider different choice of model parameters, and compare GloVe with other models. The model performance is evaluated on word analogies, word similarity and name entity recognition (NER). In summary
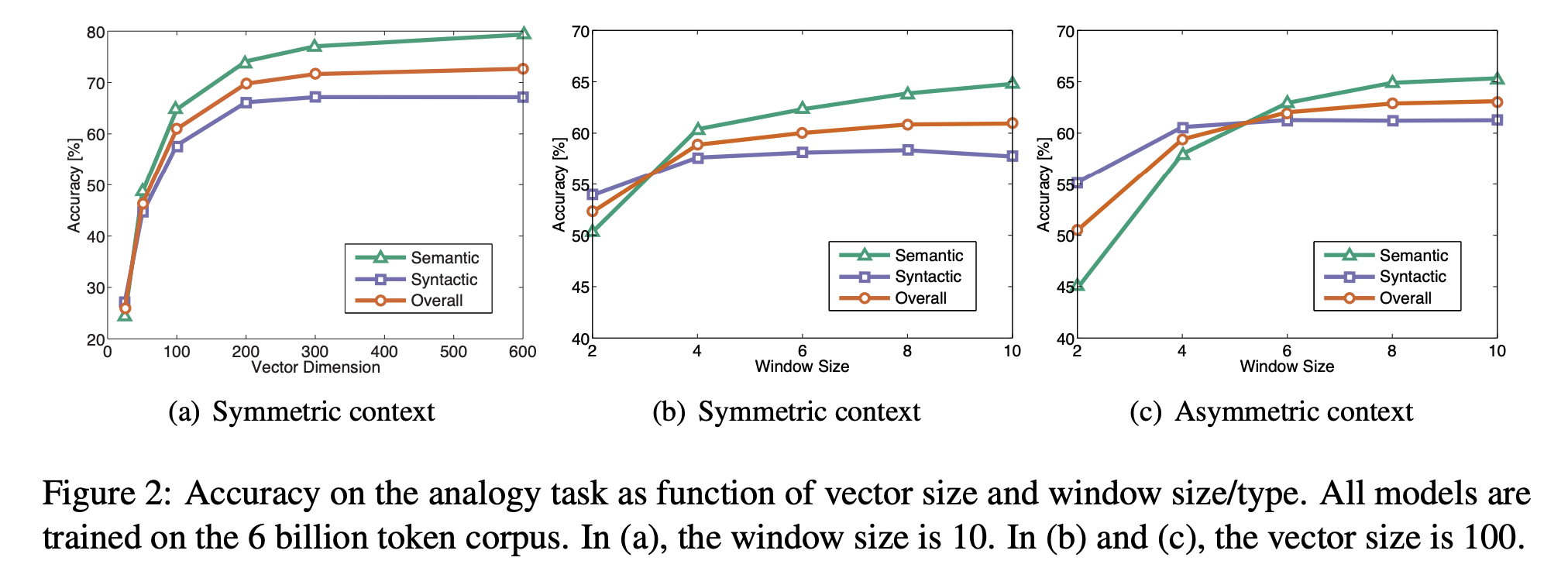
- GloVe performs better when the vector dimension is higher, but it subjects to diminishing returns for vectors greater than 200 dimensions.
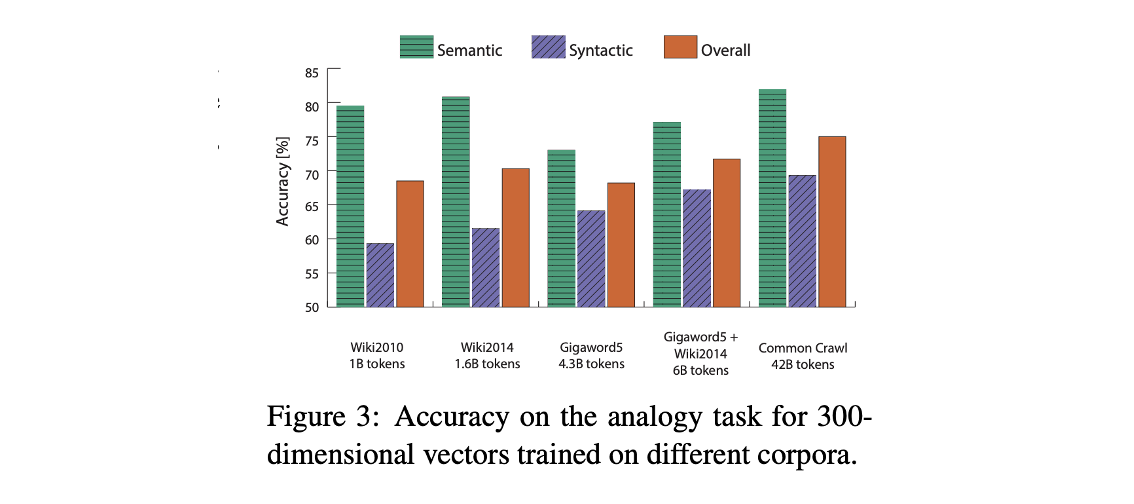
- Glove performs better then it’s trained on larger corpora, Wikipedia works better than Gigaword (news text).
- GloVe performs better on syntactic analogies with smaller and asymmetric context windows, while it performs better on semantic analogies with larger window size.
- GloVe outperforms other models in general.
Python Implementation
Now let’s play with GloVe. Here we use the pre-trained model glove-wiki-gigaword-200 from Genism. From its name, we could see that it is trained on Wikipedia and Gigaword with vector size of 200. You could also check all available models and pick one according to your need.
import gensim.downloader as api
wv_glove_200 = api.load('glove-wiki-gigaword-200')
print('Available models:', list(api.info()['models'].keys()))
Available models: ['fasttext-wiki-news-subwords-300', 'conceptnet-numberbatch-17-06-300', 'word2vec-ruscorpora-300', 'word2vec-google-news-300', 'glove-wiki-gigaword-50', 'glove-wiki-gigaword-100', 'glove-wiki-gigaword-200', 'glove-wiki-gigaword-300', 'glove-twitter-25', 'glove-twitter-50', 'glove-twitter-100', 'glove-twitter-200', '__testing_word2vec-matrix-synopsis']
After loading the model, you could get the word vector of any word in the dictionary, get the most similar words, compare the Cosine similarity and distance (1-similarity) between two words. Try following.
wv_glove_200.get_vector('boy')
print("5 most similar words to 'boy':",wv_glove_200.most_similar('boy', topn=5))
print("similarity between 'boy' and 'girl':",wv_glove_200.similarity('boy','girl'))
print("distance between 'boy' and 'girl':",wv_glove_200.distance('boy','girl'))
print("similar+distance between 'boy' and 'girl':",wv_glove_200.similarity('boy','girl')+wv_glove_200.distance('boy','girl'))
5 most similar words to 'boy': [('girl', 0.8486549258232117), ('boys', 0.7266348004341125), ('kid', 0.6983347535133362), ('man', 0.6848182082176208), ('child', 0.6708458662033081)]
similarity between 'boy' and 'girl': 0.848655
distance between 'boy' and 'girl': 0.15134501457214355
similar+distance between 'boy' and 'girl': 1.0
To evaluate the model performance on word similarity task, we could use 'wordsim353.tsv' from Gensim, which contains 353 of English word pairs with human-assigned similarity judgments. It calculates the correlation between word vector similarity and human judgments. Higher correlation indicates better model performance.
from gensim.test.utils import datapath
wv_glove_200.evaluate_word_pairs(datapath('wordsim353.tsv'))
(PearsonRResult(statistic=0.5777980353483706, pvalue=7.972715451850059e-33),
SpearmanrResult(correlation=0.5775613720052261, pvalue=8.571561605709587e-33),
0.0)
From the output, you get the Pearson and Spearman rank correlation are both around 58%, with a very low p-value (highly significant).
Let’s try another task - word analogies. A word analogy is a statement “a is to b as x is to y”, namely, a and x can be transformed in the same way to get b and y, and vice-versa. One of the most classical word analogy questions is “man is to king as woman is to what?”.
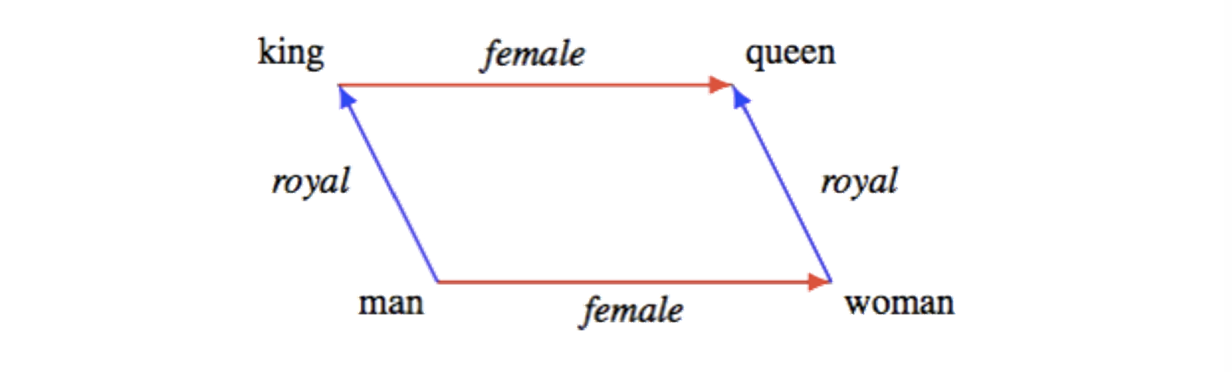
To get the answer, we can use most_similar with positive and negative. The function will return us words that are most similar to the words in the positive list (woman, king) and most dissimilar from the words in the negative list (man). In other word, it finds the optimal word x which maximizes $(w+k-m)\cdot x$, where w, k, m, x represents the word vectors for woman, king, man, and x respectively.
wv_glove_200.most_similar(positive=['woman', 'king'], negative=['man'])
[('queen', 0.6978678703308105),
('princess', 0.6081744432449341),
('monarch', 0.5889754891395569),
('throne', 0.5775108933448792),
('prince', 0.5750998258590698),
('elizabeth', 0.546359658241272),
('daughter', 0.5399125814437866),
('kingdom', 0.5318052768707275),
('mother', 0.5168544054031372),
('crown', 0.5164473056793213)]
wv_glove_200.most_similar(positive=['painter', 'drive'], negative=['paint'])
[('born', 0.45889049768447876),
('composer', 0.42856672406196594),
('drives', 0.42286112904548645),
('poet', 0.4118410348892212),
('driven', 0.4111713767051697),
('nephew', 0.4032553732395172),
('writer', 0.40040263533592224),
('father', 0.3996732532978058),
('novelist', 0.39664459228515625),
('musician', 0.3960341215133667)]
As shown in the second example, sometimes the function fails to get the correct answer. You could try other analogies by yourself, do you get it right?
Word analogy is commonly used to evaluate model performance. Google has released a testing set here of about 20,000 syntactic and semantic examples. It includes different sections, like capital-common-countries, capital-world, currency, city-in-state, family, adjective-to-adverb, opposite, comparative, superlative, ect. You can also get this from gensim, and evaluate the model performance as follow.
from gensim.test.utils import datapath
wv_glove_200.evaluate_word_analogies(datapath('questions-words.txt'))
(0.699784460638407,
[{'section': 'capital-common-countries',
'correct': [('ATHENS', 'GREECE', 'BAGHDAD', 'IRAQ'),
('ATHENS', 'GREECE', 'BANGKOK', 'THAILAND'),
('ATHENS', 'GREECE', 'BEIJING', 'CHINA'),
('ATHENS', 'GREECE', 'BERLIN', 'GERMANY'),
('ATHENS', 'GREECE', 'BERN', 'SWITZERLAND'),
('ATHENS', 'GREECE', 'CAIRO', 'EGYPT'),
('ATHENS', 'GREECE', 'CANBERRA', 'AUSTRALIA'),
('ATHENS', 'GREECE', 'HANOI', 'VIETNAM'),
('ATHENS', 'GREECE', 'HAVANA', 'CUBA'),
('ATHENS', 'GREECE', 'HELSINKI', 'FINLAND'),
('ATHENS', 'GREECE', 'ISLAMABAD', 'PAKISTAN'),
('ATHENS', 'GREECE', 'KABUL', 'AFGHANISTAN'),
('ATHENS', 'GREECE', 'MADRID', 'SPAIN'),
('ATHENS', 'GREECE', 'MOSCOW', 'RUSSIA'),
('ATHENS', 'GREECE', 'OSLO', 'NORWAY'),
('ATHENS', 'GREECE', 'OTTAWA', 'CANADA'),
('ATHENS', 'GREECE', 'PARIS', 'FRANCE'),
('ATHENS', 'GREECE', 'ROME', 'ITALY'),
('ATHENS', 'GREECE', 'STOCKHOLM', 'SWEDEN'),
('ATHENS', 'GREECE', 'TEHRAN', 'IRAN'),
('ATHENS', 'GREECE', 'TOKYO', 'JAPAN'),
('BAGHDAD', 'IRAQ', 'BANGKOK', 'THAILAND'),
('BAGHDAD', 'IRAQ', 'BEIJING', 'CHINA'),
...
('DALLAS', 'TEXAS', 'SEATTLE', 'WASHINGTON'),
('DALLAS', 'TEXAS', 'DENVER', 'COLORADO'),
('DALLAS', 'TEXAS', 'MESA', 'ARIZONA'),
('DALLAS', 'TEXAS', 'ATLANTA', 'GEORGIA'),
...]}])
From the outcome, we can learn the overall accuracy of glove-wiki-gigaword-200 model is close to 70%. It also lists the correct analogies and incorrect ones for each section, so you could calculate the accuracy per section if needed.
The main weakness of both Word2Vec and GloVe is that they do not differentiate same word in different context. Consider two sentences, “An apple a day keeps the doctor away” and “Apple launched its new iPhone 14”, does the word “apple” have same meaning? Apparently not, but it will only have 1 word vector in Word2Vec and GloVe. You could address this by labelling words with different meaning, but that will be a lot more work. A new model, ELMo (Embeddings from Language Models), solve this by considering the entire input sentence for computing the word vector. We will cover this in the future.
That’s all we have for this post. If you find it helpful and want to learn more about word embedding, stay tuned to this series, see you next time!
Reference
- Stanford CS224N | Winter 2021, recordings can be found on Youtube, highly recommended!
- Pennington et al., 2014, GloVe: Global Vectors for Word Representation
- Genism, models.keyedvectors – Store and query word vectors
- Kawin Ethayarajh, Word Embedding Analogies: Understanding King - Man + Woman = Queen
- Kovendhan Venugopal, Mathematical Introduction to GloVe Word Embedding
